|
Hooke's Law - Lesson II
Objectives
• Be able to sketch and label a graph for a material
being stretched.
• Be able to use the equation
F = k × e to solve
numerical problems involving the elastic deformation of materials.
Task 1
You should remember from last lesson that the
extension of a spring depends on the force applied.

Remind the person next to you:
• What kind of relationship exists between force and
extension.
• What features of your graph tell you this.
Task 2
Write the title "Hooke's Law" in your exercise book
and copy the sentences and formula below:
|
Below the limit of
proportionality the force is proportional to the extension and
the spring returns to its original shape when the force is removed.
This is known as the elastic region. In this region
we can use Hooke's law. |
|
F = k
× e
|
F = Force (N)
k = spring
constant (N/m)
e =
extension (m) |
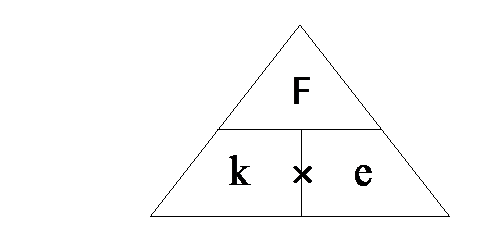
Note: the formula is given in the examination,
but the equation triangle is not given. If you find it
easier to use the equation triangle then it is up to you to remember it!
1. A spring extends by 0.15m when a force of 18N is
applied. Calculate the spring constant.
2. A trampoline has 96 springs, each of
spring constant 4500 Nm-1. One of the springs is
removed for testing, and is loaded with a weight of 900N. How far
does the spring extend?
3. A spring in a set of bathroom scales has a spring
constant of 200,000 Nm-1. The spring is compressed by
4.2mm when Mr Pascoe stands on the scales. The gravitational field
strength on Earth is 9.8 N kg-1.
a.) What is the downward
force (weight) exerted by Mr Pascoe?
b.) What is Mr Pascoe's
mass?
4. A spring in a set of kitchen scales has a spring
constant of 200 Nm-1. Calculate the extension of the
spring when 300g of flour is placed in the scales.
Extension:
5. Mr Pascoe takes the bathroom scales from Q3 on a
weekend break to the moon. The gravitational field strength on the
moon is 1.6 N kg-1.
a) What would Mr Pascoe's weight be when standing on
the moon?
b) By what distance would the spring compress?
c) If the scales are calibrated to display mass (in
kilograms) correctly on Earth, what mass would the scales read?
Task 3
Last lesson your teacher demonstrated what happens when we
stretch a spring above the limit of proportionality.
Above the limit of proportionality we are no longer in the elastic region,
but in the plastic region. We are going to collect
some data to see how the relationship between force and extension
changes in the plastic region. We will do this by stretching
copper wire, which has a much larger plastic region than a spring.
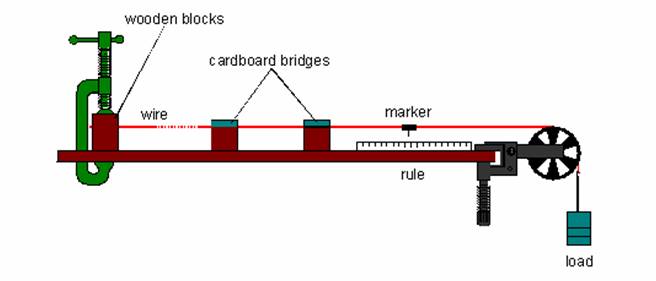
|
Note:
• The wire can snap very suddenly. Wear eye protection at all times.
• Sit at least 1.5m away from the apparatus. |
 |
Your teacher will set up the apparatus shown in the
diagram above. Draw a table, like the one below, in your exercise
book. Record the data as your teacher demonstrates the experiment.
|
Force (N) |
Extension (cm) |
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
Task 4
Plot a graph of your results.
• Force should be on the y-axis
• Extension should be on the x-axis
• Draw a suitable line of fit. There should be a
straight section to show the elastic region and a curved section to show
the plastic region, like the graph below.
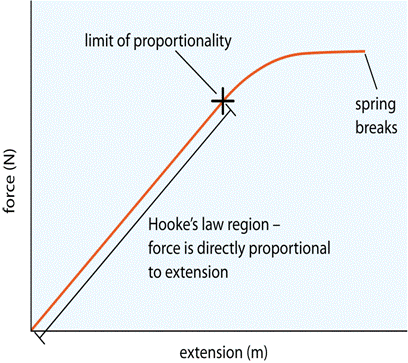
Now copy the sentences below:
Beyond the limit of proportionality
the spring permanently deforms. This is known as the plastic
region. Hooke's law does not apply in this region.
Label the elastic region, the plastic region
and the limit of proportionality on your graph and
stick it in your exercise book.
|

