Up Resources

 

                                                

 

Rogue Physicist.  Free resources for physics education © 2006-2016 Dorian Pascoe.  Email: dorian@top-school.co.uk

Most resources are available under a Creative Commons Licence.  Visit our mirror at www.physicsweb.altervista.org

 

 

Momentum - Part I

 

Objectives

• Know that all massive objects have momentum when in motion.

• Be able to calculate the momentum of a moving object using the formula p = m × v

• Be able to find the change in momentum of an object, given information about its velocity.

 

 

 

Task 1 - Starter

1. Watch this video of a tennis ball hitting the floor.  Think about the energy changes that took place, from the point the ball was released to the point it rebounds.  Discuss your ideas with the person next to you and draw an energy transfer diagram to show what happens.

 

 

2. A small rubber ball of mass 9.0g is dropped from a height of 1.25m, and lands on the ground.

 

• Calculate the change in GPE.

• State the KE of the ball at the instant it hits the floor.

• Calculate the velocity it will be travelling at this point.

• State how you would expect the velocity of rebound to compare to the velocity of impact.  Give reasons for your answer.

 

Select the correct formulae from the equation sheet.  Use g = 10 N kg-1.

 

 

 

Task 2

Watch as your teacher demonstrates a sad (inelastic) ball being dropped.  What happens when the ball strikes the table? 

 

Before collision

After collision

 

 

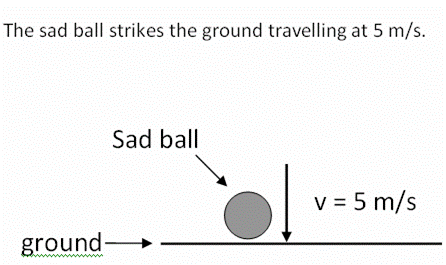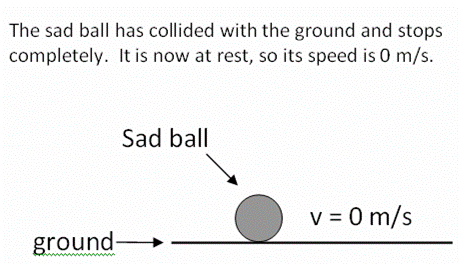Momentum is a useful quantity to help us determine the outcome of collisions.  The ball gained momentum as it fell.  When it struck the table there was a sudden change in momentum.  We can calculate the momentum of the ball at any point using the formula:

 

 

p = m × v

 

p = momentum, measured in Newton-seconds (N s or kg m/s or kg ms-1).

m = mass, measured in kilograms (kg).

v = velocity, measured in metres per second (m/s or ms-1).
 

 

Your teacher will give you a copy of the diagrams and formula above.

 

Calculate :

          • The momentum of the ball before the collision.

          • The momentum of the ball after the collision.

          • The change of momentum of the ball.

          • Is the change in momentum positive or negative?

             (Hint: is momentum lost or gained by the ball?)

 
 

Write your answers in the space on the sheet, and show full working for the calculations.

 

 

 

 

Task 3

Watch as your teacher drops the happy (elastic) ball.  The ball is the same mass, and it is dropped from the same height.  It bounces back at approximately the same speed it hits the ground.  Think about:

 

• Which quantities are different this time?

• Which quantities are the same?

• What is the momentum of the ball before the collision?

• What is the momentum of the ball after the collision?

• Will the change of momentum be bigger or smaller than the sad ball?

 

 

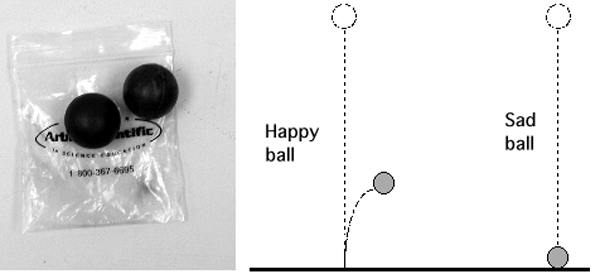
Repeat the calculations for the happy (elastic) ball.  Write your answers in the space on the sheet, and show full working for the calculations.

 

Extension / MAT work:

The happy ball does not actually bounce back at the same speed.  It has a coefficient of restitution of 0.75, meaning it will bounce back to 75% of the drop height.

 

Work out:

1. What height it will reach after bouncing.

2. What velocity it must have left the ground in order to reach this height.

3. What the change of momentum is, using your new value for velocity.

4. Assuming the bounce takes approximately 0.1 seconds, calculate:

    a) The acceleration of the ball as it undergoes the change in direction.

    b) The force exerted on the ball by the table.

 

Teacher note: The extension / MAT work is available here as a word document.

 

 

 

Task 4

Use the ideas from the work above, and the formula you have learned to solve these problems.  Answer the questions in your exercise book and show full working for all calculations.