Up Resources

 

                                                

 

Rogue Physicist.  Free resources for physics education © 2006-2016 Dorian Pascoe.  Email: dorian@top-school.co.uk

Most resources are available under a Creative Commons Licence.  Visit our mirror at www.physicsweb.altervista.org

 

 

Momentum - Part II

 

Objectives

• Know that momentum is conserved in a closed system.

• Be able to apply the law of conservation of momentum to determine the outcome of collision or explosion events.

 

 

 

 

Task 1 - Starter

Calculate:

a) The momentum of a 50kg student running at 4 m/s.

b) The momentum of a 2500g radio controlled car travelling at 6m/s.

c) The change of momentum of a 1500kg car accelerating from 10 m/s to 25 m/s.

 

 

 

 

Task 2

Momentum is a useful quantity to help us predict the outcome of collision or explosion events.  In a closed system, momentum can be transferred between objects, but the total momentum is always conserved - even if energy is lost to the surroundings.  This is known as "the law of conservation of momentum".

 

This can be expressed simply as:

"total momentum before = total momentum after"

 

Your teacher will show you a few examples of momentum being transferred in collisions, either with demonstrations or using the simulation below.

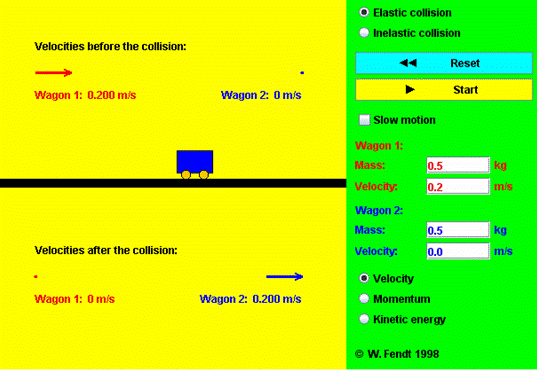
(click on the image, or this link to open the simulation in a new window.)

 

 

 

 

Task 3

The Law of Conservation of momentum is used in conjunction with the momentum formula from last lesson:

 

p = m × v

 

p = momentum, measured in Newton-seconds (N s or kg m/s or kg ms-1).

m= mass, measured in kilograms (kg).

v = velocity, measured in metres per second (m/s or ms-1).

 

 
We are going to try applying the law of conservation of momentum to find the outcome of several collision events.  Your teacher will explain how to solve the example problem below:

 

Example 1

A red billiard ball of mass 0.15kg is initially at rest, and is struck by the cue ball, which is moving at a velocity of 8m/s to the right and has a mass of 0.17kg.  The cue ball continues with a velocity of 0.5m/s to the right.  What velocity does the red ball move away?

 

You will need to:

          • Draw diagrams showing the 'before' and 'after' scenarios.

          • Calculate the momentum of each object before the collision.

          • Calculate the total momentum before the collision.

          • Calculate the momentum of the cue ball after the collision.

          • Find the momentum transferred to the red ball.

          • Find the velocity of the cue ball using p = m x v.

 

 

 

 

Example 2

 

An __________ of mass ___________ is moving... etc!

 

 

You teacher will help you to draw diagrams showing the 'before' and 'after' scenarios and to label all known and unknown quantities.

 

You will need to:

          • Calculate the momentum of each object before the collision.

          • Calculate the total momentum before the collision.

          • Calculate the momentum of the ________ after the collision.

          • Find the momentum transferred to the _________.

          • Find the _________ of the ________ using p = m x v.

 

 

 

 

 

 

 

Task 4

Apply the law of conservation of momentum to solve these problems.  You will need to draw clearly labelled 'before' and 'after' diagrams for each question to help you solve the problem.  Show full working for all your calculations.

 

 

Extension / MAT work:

Consider the case of object, of mass "m" in motion at an initial velocity "vo" striking an object of equal mass, which is initially at rest.  Show that, in a completely inelastic collision where the two objects stick together, they will move away with half the initial velocity of the first object.

 
 

 

 

 

Homework

Complete these momentum problems.  Draw 'before' and 'after' diagrams for each problem, and show full working for your calculations.